가우시안 프로세스에 대한 간단한(?) 설명
2023/01/17
(주의: 이 글에서 다루는 내용은 통계학 중급자 이상을 대상으로 하는 내용으로, 좀 어렵습니다. 특히 베이즈 정리, 다변량 정규분포와 그에 관련된 행렬 이론에 대한 이해를 필요로 합니다.)
요청이 있어서, 가우시안 프로세스 (Gaussian Process) 라는 것에 대해 제가 최근 공부한 것을 바탕으로 최대한 간략하게 소개하려 합니다. 가우시안 프로세스는 이름에서 알 수 있듯 정규분포, 특히 다변량 정규분포를 기반으로 하는 방법론입니다. 이 방법론은 다양한 응용 분야를 갖고 있는 듯한데, 딥러닝이 등장하기 이전까지는 꽤 인기있는 머신러닝 프레임웍이었던 듯하고, 지금도 머신러닝 모델의 파라미터 튜닝을 위해 흔히 사용되는 듯합니다 특히 베이지안 최적화 (Bayesian optimization) 와 관련해서 말이죠.
그리고 지금부터는 가우시안 프로세스를 줄여서 GP라고 부르기로 하겠습니다.
1. 동기
GP에 대해 이해하기 위해서는 애초에 이 방법론이 왜 필요한지 소개하는 것이 큰 도움이 될듯합니다. 우리가 즐겨 사용하는, 가장 초보적인 회귀분석 기법은 역시 선형회귀일텐데요, 잘 아시듯 선형회귀분석은 반응변수의 기댓값을 설명변수 또는 피쳐 (feature) 의 선형결합으로 표현하는 기법입니다. 그런데 당연하게도, 현실 세계에서 피쳐와 반응변수 간의 관계는 선형이 아닌 경우가 아주 많습니다. 이런 경우에는 당연히 선형회귀분석이 잘 작동하지 않습니다.
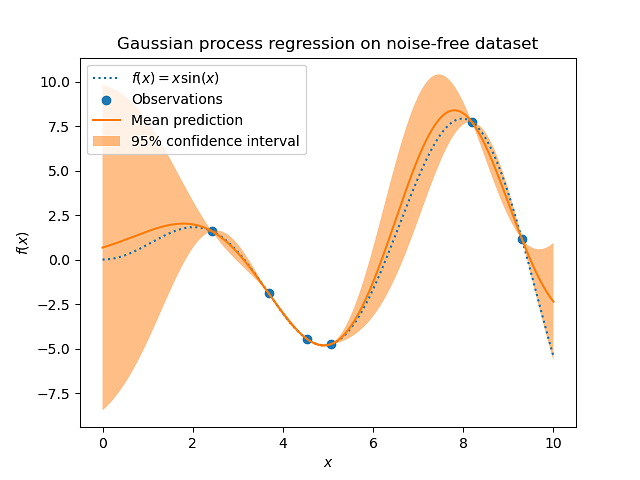
비교적 간단한 예를 들어 다음과 같은 관계를 생각해볼 수 있습니다.
y = sin(x) + e, e ~ N(0, sigma^2)
그러니까 반응변수는 설명변수 하나에 대한 사인함수에 노이즈를 더한 것으로 표현됩니다. 이런 관계는 당연하게도 선형적인 관계가 아니고...

심리학을 전공했지만 졸업 후에는 미국에서 데이터과학자로 일하고 있습니다. 데이터를 가지고 가치 있는 활동을 하는 데 관심이 많습니다. [가짜뉴스의 심리학], [3일 만에 끝내는 코딩 통계], [데이터과학자의 일] 등을 썼습니다.














.jpg)


늦게나마 자세히 읽게 되었는데 정말 잘 읽었습니다!! 최근에 개인적으로 기계학습 이론을 공부하면서, Neural network as gaussian process (NNGP)라는 것을 보게 되었는데 처음에는 그 의미를 잘 몰랐었습니다. 통계학은 잘 모르는 입장에서 Gaussian process라는 단어를 보면 말 그대로 Gaussian 분포를 갖는 확률과정인가보다 라는 생각만 들었고, 그것에 기반한 어떤 구체적인 통계학적 기법을 말한다는 것을 몰랐기 때문인데요
그러던 와중에 문득 이 글을 본 기억이 나서 접속해서 읽어보면서, GP라는 것이 가우시안 확률과정을 이용해서 베이즈추론 맥락에서 함수를 맞추어주는 통계적 예측 기계를 일컫는다는 것을 처음 알게 되었습니다. 특히 글에서 소개해주신 조건부확률의 평균 \bar\mu와 분산 \bar\Sigma에 대한 공식이, posterior 확률 분포를 실제로 계산해서 얻을 수 있게 해주므로 중요한것 같습니다.
따라서 상술한 NNGP에서 이야기하는 것은 결국 이상적인 neural network는 가우시안 프로세스로서 Bayesian inference를 수행한다 라는 얘기인 것 같습니다. 아무쪼록 좋은 글 써주셔서 다시한번 감사합니다.
확률분포 기반의 예측 모델에 아름다움을 다시 한 번 느끼고 갑니다. ㅎㅎ
@클레이 곽 이 글은 요청이 있어서 쓴 상당히 어려운 내용에 대한 글입니다. 다른 글들은 이렇게 어렵지 않을겁니다.
와이너 가우시안프로세스 브라우니언무브먼트 석사때 저에게 최악의 점수를 안겨줬던...
와 너무 어렵습니다. 수학을 싫어해서 경영대학내에서 경제학과 갔다가 통계학때문에 고생했는데.... 여기서 또봅니다...ㅎㅎㅎ 그래도 자꾸 올려주시면 다시 수학과 통계학을 공부해보겠습니다.
와이너 가우시안프로세스 브라우니언무브먼트 석사때 저에게 최악의 점수를 안겨줬던...
와 너무 어렵습니다. 수학을 싫어해서 경영대학내에서 경제학과 갔다가 통계학때문에 고생했는데.... 여기서 또봅니다...ㅎㅎㅎ 그래도 자꾸 올려주시면 다시 수학과 통계학을 공부해보겠습니다.