중심극한정리는 당신의 모집단을 마법처럼 정규분포로 바꾸어 주지 않습니다.

산업/기술/IT
박준석
박준석 인증된 계정 · 데이터 사이언티스트입니다.
2023/01/07
사회과학에만 유령이 있는 게 아닙니다. 통계학에도 하나의 아주 악명높은 유령이 있습니다. 바로 중심극한정리라는 유령. 이 유령을 퇴치하기 위해 지금까지 수많은 통계학자와 데이터분석가가 덤볐지만, 끈질기게 죽지도 않고 살아납니다. 아니면 애초에 죽었으니 다시 죽일 수가 없는 것일까요. 그래서인지 여태 이 유령을 완전히 퇴치할 수는 없었습니다. 그래서 데이터분석을 하는 사람들은 주기적으로 되새겨야 합니다. 중심극한정리가 무엇인가를. 그래야 이 유령에게 홀리지 않을 수 있습니다. 

아니, 사실 그 유령은 중심극한정리 그 자체가 아닙니다. 정확히 말하자면, 그 죽지도 않고 또 온 유령은 표본 크기가 충분히 크면, 중심극한정리에 의해 모집단이 정규분포를 따른다 입니다. 통계학에 조금의 관심이라도 있다면, 여러분도 이런 진술을 어디선가 봤을 것입니다. 이런 틀린 진술을. 제가 이 글을 쓰게 된 계기도 최근 이런 진술을 어디선가 또 봤기 때문입니다. 그것도 시중에서 꽤 잘 팔리고 있는 듯한 책에서 말이죠. 그 책 자체는 전반적으로 꽤 잘 쓴 책으로 보이고, 판매도 꽤 되고 있는 것 같습니다. 하지만 이 잘못된 명제 하나 때문에 저 같은 프로불편러의 역린을 건드려 버렸습니다.
 
이 글에서는 이 진술이 어디가 틀렸는지, 그리고 정확한 버전은 무엇인지 짧게 설명하겠습니다. 수식은 등장하지 않으니 걱정 안 하셔도 됩니다. 하지만 이 글에서 강조하려는 것은 이런 것들보다는 애초에 이런 오해가 왜 생기게 되었느냐 하는 것입니다. 사실 이것이 본질입니다. 

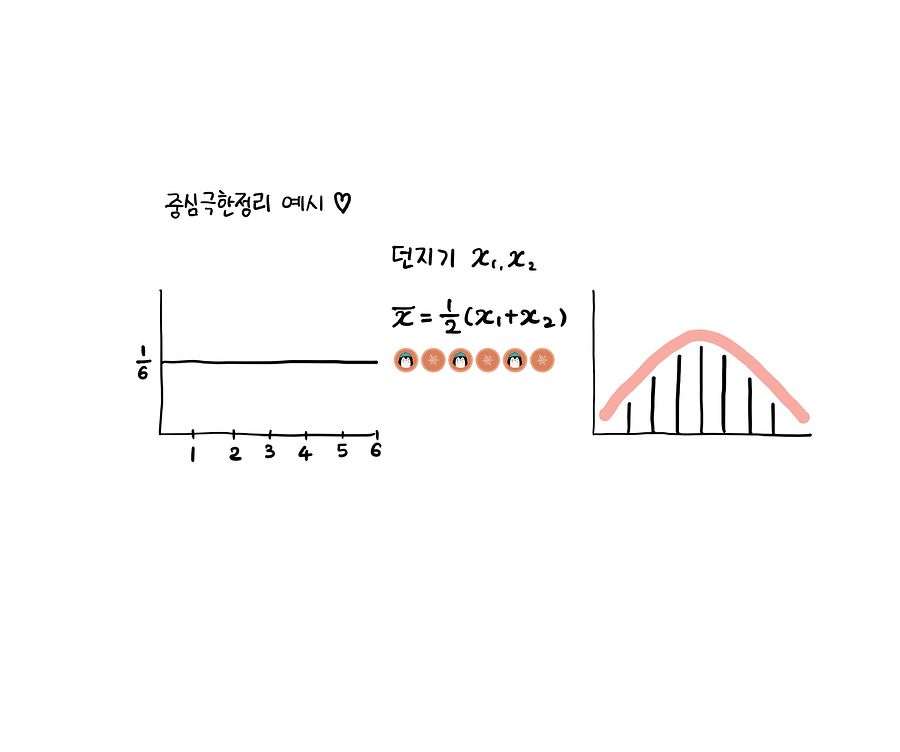
먼저 중심극한정리는 기본적으로 우리가 관심있어하는 집단 (모집단) 자체가 아니라 표집분포 또는 표본평균의 분포에 관한 명제입니다. 이 둘 (모집단의 분포 / 표집분포) 을 구분하지 못하는 것, 나아가 표본평균 같은 통계량이 그 자체의 분포를 가질 수 있다는 것 자체를 상상하지 못하는 것이 오해의 근본적인 원인입니다. 따라서 이 두 가지를 확실하게 구분하는 것이 중심극한정리에 대한 오해를 해결하는 첫걸음입니다. 

우선 모집단입니...
박준석
박준석 님이 만드는
차별화된 콘텐츠, 지금 바로 만나보세요.
가입하고 이어읽기
이미 회원이신가요? 로그인
박준석
박준석 인증된 계정
데이터 사이언티스트입니다.
심리학을 전공했지만 졸업 후에는 미국에서 데이터과학자로 일하고 있습니다. 데이터를 가지고 가치 있는 활동을 하는 데 관심이 많습니다. [가짜뉴스의 심리학], [3일 만에 끝내는 코딩 통계], [데이터과학자의 일] 등을 썼습니다.
글 24
팔로워 2.5K
팔로잉 31
끼니
홈은
몬스