내적 (dot product) 과 그 기하학적 의미, 통계/기계학습과의 관련성
2023/04/17
오늘은 좀 가벼운(?) 주제에 대해 이야기해볼까 한다. 바로 벡터 간의 곱에 대한 이야기다. 아는 사람들은 다 아는 이야긴데 벡터 간의 곱셈은 통계학과 기계학습에서 엄청나게 자주 등장하고 중요한 개념이다. 그런데 중요한 건 그게 어떤 기하학적 의미를 갖는다는 것이고, 이를 잘 이해하면 통계/기계학습 관련 개념 이해에 무진장 도움이 된다는 것이다. 그래서 오늘은 짧게 이 얘기를 해 보려고 한다.
(주의: 두 벡터를 곱하는 방법은 한 가지가 아니다. 그래서 이 글에서 말하는 곱셈이 두 벡터를 곱하는 유일한 방법이라고 오해하면 안 된다.)
먼저 벡터 간의 곱셈이 뭔지부터 얘기를 해야 할 것 같다. 그러기 위해서는 벡터가 뭔지 얘기를 해야 한다. 벡터는 쉽게 말하면 그냥 숫자를 죽 한 줄로 나열한 것이다. 이를테면 다음과 같은 것은 벡터다 (대개 벡터를 쓸 때는 괄호 안에 숫자를 죽 나열한다).
(1, 2, 3, ..., 10)
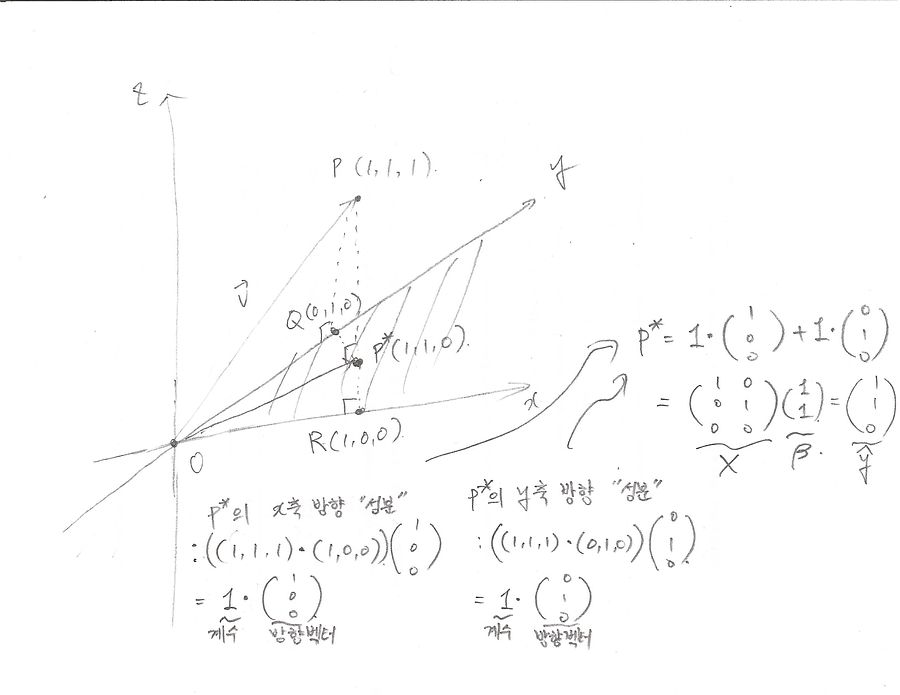
자, 그럼 이제 벡터 얘기를 다 했다. 놀랍겠지만 이 이상 할 얘기가 별로 없다. 아, 사실 하나 빼먹은 게 있긴 하다. 바로 벡터는 그래프로 나타냈을 때 공간상의 점이 된다는 것이다. 아마 중/고등학교에서 (1, 2)는 x=1, y=2라는 2차원 상의 점에 대응된다는 것을 배웠을 것이다. 이 얘기를 3차원으로도 확장할 수 있고 사실 몇 차원으로 확장하든 다 성립하는 얘기다. 그런데 4차원 이상이면 우리의 지각 능력으로는 시각화할 수 없을 따름이다.
그럼 이제 본론으로 돌아가서, 사실 통계/기계학습에서 가장 많이 쓰는 벡터 간의 곱셈은 dot product라 부르는 것이다. 우리말로는 내적이라고 옮기는 것 같다. 두 벡터가 있을 때, 내적은 대응되는 위치에 있는 숫자들끼리 일단 곱한 다음 그 결과를 다 더하는 것이다. 이를테면 다음의 두 벡터의 내적은
x=(1,2), y=(3,4)
일단 대응되는 위치에 있는 숫자끼리 곱하면 3,8을 얻고, 이 숫자들을 다 더하면 11이 나온다. 그냥 이게 끝이다. 간단하지 않은가?
근데 지금부터가 재밌다. 당연히 벡터...
(주의: 두 벡터를 곱하는 방법은 한 가지가 아니다. 그래서 이 글에서 말하는 곱셈이 두 벡터를 곱하는 유일한 방법이라고 오해하면 안 된다.)
먼저 벡터 간의 곱셈이 뭔지부터 얘기를 해야 할 것 같다. 그러기 위해서는 벡터가 뭔지 얘기를 해야 한다. 벡터는 쉽게 말하면 그냥 숫자를 죽 한 줄로 나열한 것이다. 이를테면 다음과 같은 것은 벡터다 (대개 벡터를 쓸 때는 괄호 안에 숫자를 죽 나열한다).
(1, 2, 3, ..., 10)
자, 그럼 이제 벡터 얘기를 다 했다. 놀랍겠지만 이 이상 할 얘기가 별로 없다. 아, 사실 하나 빼먹은 게 있긴 하다. 바로 벡터는 그래프로 나타냈을 때 공간상의 점이 된다는 것이다. 아마 중/고등학교에서 (1, 2)는 x=1, y=2라는 2차원 상의 점에 대응된다는 것을 배웠을 것이다. 이 얘기를 3차원으로도 확장할 수 있고 사실 몇 차원으로 확장하든 다 성립하는 얘기다. 그런데 4차원 이상이면 우리의 지각 능력으로는 시각화할 수 없을 따름이다.
그럼 이제 본론으로 돌아가서, 사실 통계/기계학습에서 가장 많이 쓰는 벡터 간의 곱셈은 dot product라 부르는 것이다. 우리말로는 내적이라고 옮기는 것 같다. 두 벡터가 있을 때, 내적은 대응되는 위치에 있는 숫자들끼리 일단 곱한 다음 그 결과를 다 더하는 것이다. 이를테면 다음의 두 벡터의 내적은
x=(1,2), y=(3,4)
일단 대응되는 위치에 있는 숫자끼리 곱하면 3,8을 얻고, 이 숫자들을 다 더하면 11이 나온다. 그냥 이게 끝이다. 간단하지 않은가?
근데 지금부터가 재밌다. 당연히 벡터...

심리학을 전공했지만 졸업 후에는 미국에서 데이터과학자로 일하고 있습니다. 데이터를 가지고 가치 있는 활동을 하는 데 관심이 많습니다. [가짜뉴스의 심리학], [3일 만에 끝내는 코딩 통계], [데이터과학자의 일] 등을 썼습니다.
















.jpg)


아주 흥미롭게 읽었습니다. 시리즈로 계속 풀어 주셔도 독창적인 글이 될 것 같습니다. +_+
'x축 위'라는 표현과 'x축보다 위'라는 말 사이에 잠시 혼동이 왔지만 영혼을 붙잡으며 흥미롭게 읽었습니다. 취미로서의 수학에 관심 있는 사람으로서 앞으로의 글이 기대되네요.
아주 흥미롭게 읽었습니다. 시리즈로 계속 풀어 주셔도 독창적인 글이 될 것 같습니다. +_+
'x축 위'라는 표현과 'x축보다 위'라는 말 사이에 잠시 혼동이 왔지만 영혼을 붙잡으며 흥미롭게 읽었습니다. 취미로서의 수학에 관심 있는 사람으로서 앞으로의 글이 기대되네요.